概念~

二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

任意节点的左、右子树也分别为二叉查找树；

没有键值相等的节点。

优势~O(log n)

　　二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低——为O(log n)。

　　二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等。

　　二叉查找树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉查找树变成一个有序序列，构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。

搜索、插入、删除的复杂度等于树高，期望 $O(\log n)$ ，最坏 $O(n)$ （数列有序，树退化成线性表）。

　　虽然二叉查找树的最坏效率是O(n)，但它支持动态查询，且有很多改进版的二叉查找树可以使树高为 $O(\log n)$ ,如,，等。

　　故不失为一种好的动态查找方法。

　　其中C++的STL中的set就是使用的红黑树作为存储结构的（ps：hash_set使用的是hash_table作为存储结构）

Search BST

在二叉搜索树b中查找x的过程为：

若b是空树，则搜索失败，否则：

若x等于b的根节点的数据域之值，则查找成功；否则：

若x小于b的根节点的数据域之值，则搜索左子树；否则：

查找右子树。

1 /* 以下代码为C++写成，下同*/ 2 Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p){ 3   //在根指针T所指二元查找樹中递归地查找其關键字等於key的數據元素，若查找成功， 4   //則指针p指向該數據元素節點，并返回TRUE，否則指针指向查找路徑上訪問的最後 5   //一個節點并返回FALSE，指针f指向T的雙親，其初始调用值為NULL 6   if(!T) { //查找不成功 7     p=f; 8     return false; 9   }10   else if (key == T->data.key) { //查找成功11     p=T;12     return true;13   }14   else if (key < T->data.key) //在左子樹中繼續查找15     return SearchBST(T->lchild, key, T, p);16   else //在右子樹中繼續查找17     return SearchBST(T->rchild, key, T, p);18 }

InsertBST

向一个二叉搜索树b中插入一个节点s的算法，过程为：

若b是空树，则将s所指结点作为根节点插入，否则：

若s->data等于b的根节点的数据域之值，则返回，否则：

若s->data小于b的根节点的数据域之值，则把s所指节点插入到左子树中，否则：

把s所指节点插入到右子树中。（新插入节点总是叶子节点）

1 /*当二元搜尋樹T中不存在关键字等于e.key的数据元素时，插入e并返回TRUE，否则返回FALSE*/ 2 Status InsertBST(BiTree *T, ElemType e){   3       if(!T)   4         {         5             s = new BiTNode; 6             s->data = e; s->lchild = s->rchild = NULL; 7             T=s;    //被插節点*s为新的根结点 8         } 9       else if(e.key == p->data.key)10         return false;//关键字等于e.key的数据元素，返回錯誤11       if (e.key < p->data.key)12     InsertBST(p->lchild, e);    //將e插入左子樹13       else 14     InsertBST(p->rchild, e);    //將e插入右子樹15       return true;16  }

DeleteBST

在二叉查找树删去一个结点，分三种情况讨论：

若*p结点为叶子结点，即PL（左子树）和PR（右子树）均为空树。由于删去叶子结点不破坏整棵树的结构，则只需修改其双亲结点的指针即可。

若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉查找树的特性。

若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：其一是令*p的左子树为*f的左/右（依*p是*f的左子树还是右子树而定）子树，*s为*p左子树的最右下的结点，而*p的右子树为*s的右子树；其二是令*p的直接前驱（in-order predecessor）或直接后继（in-order successor）替代*p，然后再从二叉查找树中删去它的直接前驱（或直接后继）。

在二叉查找树上删除一个结点的算法如下：

1 Status DeleteBST(BiTree *T, KeyType key){ 2   //若二叉查找树T中存在关键字等于key的数据元素时，则删除该数据元素，并返回 3   //TRUE；否则返回FALSE 4   if(!T)  5     return false;    //不存在关键字等于key的数据元素 6   else{ 7     if(key == T->data.key) {     //  找到关键字等于key的数据元素 8       return Delete(T); 9     }10     else if(key < T->data.key)11       return DeleteBST(T->lchild, key);12     else13       return DeleteBST(T->rchild, key);14   }15 }16 17 Status Delete(BiTree *p){18   //该节点为叶子节点，直接删除19   BiTree *q, *s;20   if (!p->rchild && !p->lchild)21   {22       delete p;23       p = NULL;24   }25   else if(!p->rchild){    //右子树空则只需重接它的左子树26     q=p->lchild;27     p->data = p->lchild->data;28     p->lchild=p->lchild->lchild;29     p->rchild=p->lchild->rchild;30 31     delete q;32   }33   else if(!p->lchild){    //左子树空只需重接它的右子树34     q=p->rchild;35     p->data = p->rchild->data;36     p->lchild=p->rchild->lchild;37     p->rchild=p->rchild->rchild;38 39     delete q;  }40   else{    //左右子树均不空41     q=p; 42     s=p->lchild;43     while(s->rchild){ 44       q=s; 45       s=s->rchild;46     }    //转左，然后向右到尽头47     p->data = s->data;    //s指向被删结点的“前驱”48     if(q!=p)    49       q->rchild = s->lchild;    //重接*q的右子树50     else 51       q->lchild = s->lchild;    //重接*q的左子树52     delete s;53   }54   return true;55 }

Python版

binary_tree_delete

1 def find_min(self):   # Gets minimum node (leftmost leaf) in a subtree 2     current_node = self 3     while current_node.left_child: 4         current_node = current_node.left_child 5     return current_node 6  7 def replace_node_in_parent(self, new_value=None): 8     if self.parent: 9         if self == self.parent.left_child:10             self.parent.left_child = new_value11         else:12             self.parent.right_child = new_value13     if new_value:14         new_value.parent = self.parent15 16 def binary_tree_delete(self, key):17     if key < self.key:18         self.left_child.binary_tree_delete(key)19     elif key > self.key:20         self.right_child.binary_tree_delete(key)21     else: # delete the key here22         if self.left_child and self.right_child: # if both children are present23             successor = self.right_child.find_min()24             self.key = successor.key25             successor.binary_tree_delete(successor.key)26         elif self.left_child:   # if the node has only a *left* child27             self.replace_node_in_parent(self.left_child)28         elif self.right_child:  # if the node has only a *right* child29             self.replace_node_in_parent(self.right_child)30         else: # this node has no children31             self.replace_node_in_parent(None)

in-order-traversal

1 def traverse_binary_tree(node, callback):2     if node is None:3         return4     traverse_binary_tree(node.leftChild, callback)5     callback(node.value)6     traverse_binary_tree(node.rightChild, callback)

构造一颗二叉排序树（）

1 def build_binary_tree(values): 2     tree = None 3     for v in values: 4         tree = binary_tree_insert(tree, v) 5     return tree 6  7 def get_inorder_traversal(root): 8     ''' 9     Returns a list containing all the values in the tree, starting at *root*.10     Traverses the tree in-order(leftChild, root, rightChild).11     '''12     result = []13     traverse_binary_tree(root, lambda element: result.append(element))14     return result

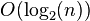每个结点的 $C_i$ 为该结点的层次数。最坏情况下，当先后插入的关键字有序时，构成的二叉查找树蜕变为单支树，树的深度为 $n$ ，其平均查找长度为 $\frac{n+1}{2}$ （和顺序查找相同），最好的情况是二叉查找树的形态和折半查找的判定树相同，其平均查找长度和 $\log_2(n)$ 成正比（ $O(\log_2(n))$ ）。

本文转自ZH奶酪博客园博客，原文链接：http://www.cnblogs.com/CheeseZH/p/5283510.html，如需转载请自行联系原作者